Quick Links
Sidebar
Deblending via sparse Stolt Transforms (Amr Ibrahim)
Simultaneous source seismic data obtained with random firing times can be separated via the application of robust denoising methods to common receiver gathers (CRG). Source interferences manifest as erratic noise in CRGs and the goal is to develop a robust apex shifted hyperbolic radon transform (ASHRT) tto remove erratic noise in CRGs. The process entails minimizing the cost function
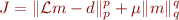
where  is the Radon operator,
is the Radon operator,  are the coefficients in Radon space that model the data
are the coefficients in Radon space that model the data  and
and  is the regularization parameter. Our algorithm adopts
is the regularization parameter. Our algorithm adopts 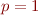 (sparse solution) and
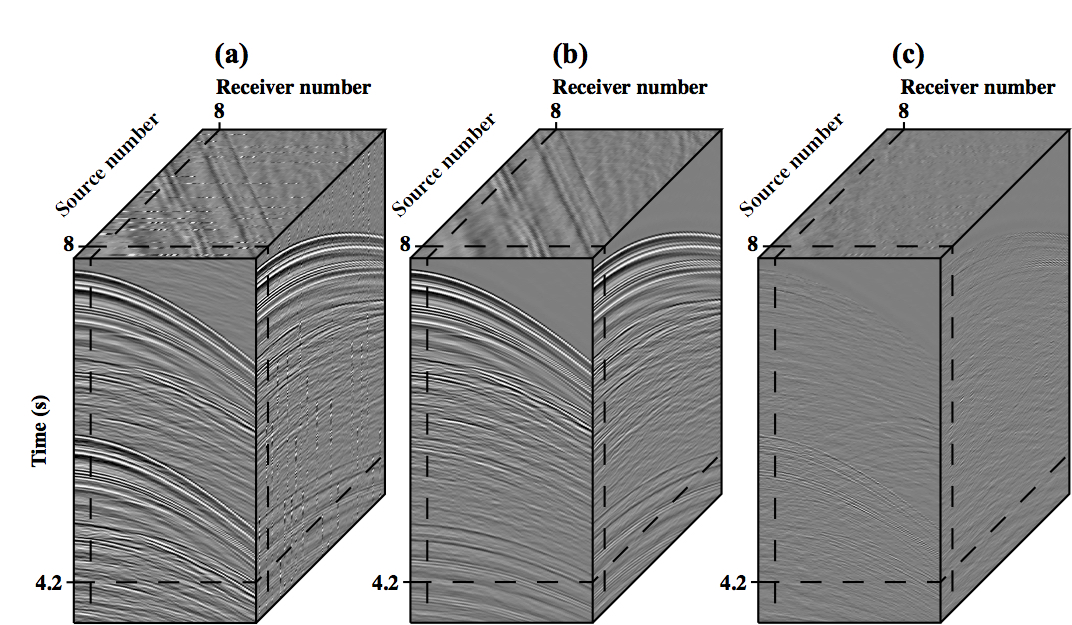
(sparse solution) and 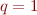 (robust solution) to denoise CRGs. Figure 1 shows the Radon panel associated to the real data cube in Figure 2. Figure 2 shows the data obtained via a simulated simultaneous source acquisition, the denoised data and the
reconstruction error.
(robust solution) to denoise CRGs. Figure 1 shows the Radon panel associated to the real data cube in Figure 2. Figure 2 shows the data obtained via a simulated simultaneous source acquisition, the denoised data and the
reconstruction error.
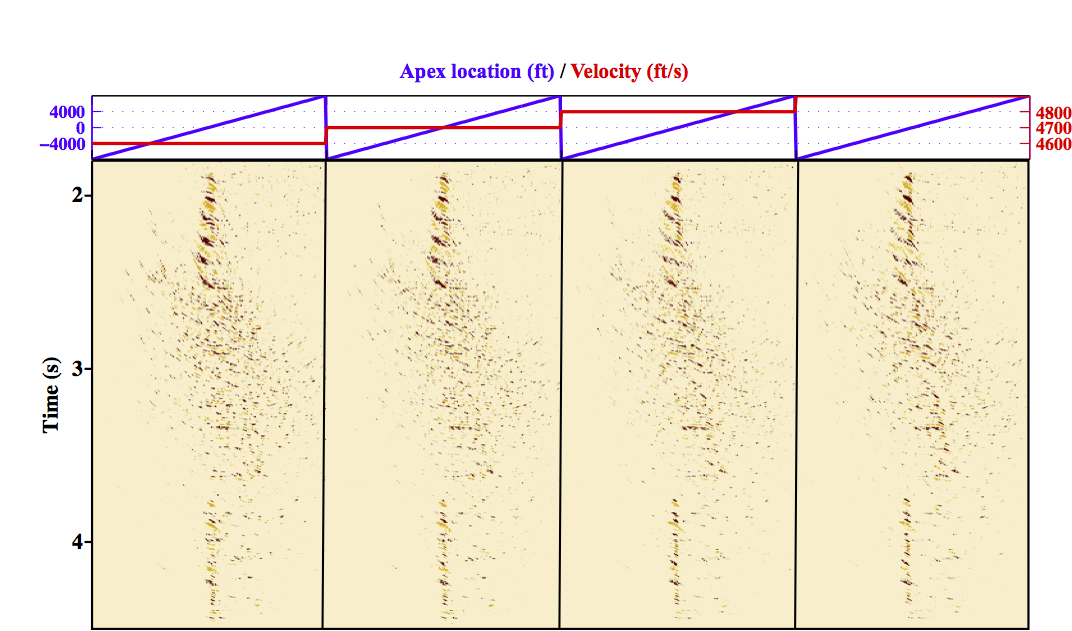 Figure 1. Four velocity panels of the field data ASHRT model. The inversion used the parameters p = 1 and q = 1.
Figure 1. Four velocity panels of the field data ASHRT model. The inversion used the parameters p = 1 and q = 1.
A Ibrahim, MD Sacchi, 2015, Fast simultaneous seismic source separation using stolt migration and demigration operators, Geophysics External Link